sums will set you free

how to teach your child numbers arithmetic mathematics

counting, addition

The approach to teaching mathematics and other languages is profoundly unsound, but the habits are deeply ingrained.

I have already provided documents explaining where the problems are on a technical and adult level. To dig into this, start at why Aristotelian logic does not work and laying the foundations for sound education.

This sub-section of abelard.org is designed to lay out a rational and logical base for teaching arithmetic and mathematics from basics. I shall not always justify the methods in this section as I go along, but the methods are very relevant and purposefully structured. Throughout this section, many of the yellow links take you to a more advanced, or technical, explanation.

It is vital to understand that there is no fundamental or logical difference between the symbolism of teaching English and teaching arithmetic/mathematics. This congruence becomes part of the learner’s understanding. It is a deep and dangerous pedagogical error to allow the learner to imbibe the erroneous concept that mathematics and English are different “subjects”.

On these pages, you will be given basic methodology and necessary examples. You will not be provided with hundreds of examples, those you make up as you work with the learner, adjusting those examples according to the person’s problems. Some examples should be interspersed which are easy for the learner, in order to reinforce and to give experience of success, while others should be aimed at specific difficulties.

2. Counting

Numbers are a series of magical human grunts that are taught in order. Words have been assigned meaning by a more or less random process. It doesn’t matter why an object is called a duck or a table, all that is necessary is that humans recognise and remember which sound (grunt) associates with which generalised object.

The grunt ‘one’ has meaning synonymous with ‘object’, ‘thing’, ‘it’, ‘that’.
‘Two’ means another object, or object plus object, or just object object;
‘Three’ is object object object, or thing thing thing; and so on.

The numbers perform functions similar to any other words. They are not special, they are not different, however much the development of number helps humans to communicate and to develop civilisation.

3. Counting with things

The objective is to remember the numbers in order, but it is important to associate these numbers with counting objects or things. So sometimes counting fence posts, or cars, or apples, and at other times chanting these numbers in various rhythms, is useful and fun.

Notice the convenience of the numbers (digits). They are just a shorthand for spelling the word out each time, a way of keeping things neater and more uniform.

As you cannot see what is in someone else’s mind, for clear communication it is necessary to point to objects in the real world. These are objects outside your mind, which a person trying to understand you or whom you are trying to teach, can see or observe for themselves.

When in difficulties, always use referents. (A referent is an object to which you refer.)

For convenience, we are going to use fairly uniform objects like, for instance, the smallest (one unit) Cuisinaire rods.

Do this teaching of the order of the numbers by pointing to one block and then moving to the next block and stopping, then moving to the next block and stopping. If necessary, hold the child’s pointing hand in your own and move from item to item. Your are teaching the child to separate objects, but never lose sight of the fact that the world is continuous.

The cloth, or the table, with the objects is one. The tree with the leaves is one. Your hand movements are continuous. (Your hand does not disappear between the objects.) Your hand just changes the rate of movement from between the objects to resting at the objects. It is going to be important that your child learns that continuous and steps are just two ways of looking at the same world.

one, object, thing, it, that 1		two, one two 1, 2 on object and another object, or object plus object, or just object object
three, one two three 1, 2, 3 object plus object plus object, or just object object object		four, one two three four 1, 2, 3, 4 object plus object plus object plus object, or just object object object object

and so on.

As you will see below, we are counting blocks. Here is a cloth with no blocks upon it.

Some people call this nothing or zero, but we know that we have a cloth on the table, on the floor, on the world. We just do not yet have any blocks on the cloth. Thus, we just have no blocks or zero blocks, or zero elephants, or zero cars.

For more, see counting in the real world.

abelard.org maths educational counter

[This counter functions with javascript, you need to ensure that javascript is enabled for the counter to work.]

The full version with more detailed instructions, go to the introduction page.

At this early stage, the counter is used to show the numbers counting upwards, or later in the page to watch counting in twos.

You can, of course, play around with the counter if you wish, and you’ll find you can do some pretty complicated and weird sums, if that sort of thing gives you joy. If you’re really determined, you can even make the counter say “NaN”, or “Not a Number”. That’s an error message telling you that you’ve done something silly. ☺

Below is a concise version of the Brilliant abelard.org eduacational maths counter. For an expanded version with more detailed instructions, go to how to teach your child number arithmetic mathematics - introduction.

[This counter functions with javascript, you need to ensure that javascript is enabled for the counter to work.]

Addition

So now we move one block onto one cloth and two blocks onto another cloth (or even the same cloth at a different time).

one       two three

Count the blocks on each cloth. Now draw the two cloths together.

one two three

Now count all the blocks on both the cloths, straight through without stopping. You have three blocks, that is block, block, block; it, it, it; three blocks.

Similarly, we have three blocks and five blocks.
one two three	four five six seven eight		one two three four five six seven eight

Now when you count through, you will find you have eight blocks,

or even spoons,

or even potatoes.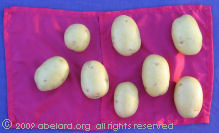

You teach the numbers to the child as you are walking along the street, or you are washing the dishes, or sowing the carrot seeds. How many cups are there to wash? illus You have the idea, make up your sums to the degree needed for the child to become fluent and confident. Obviously, you make up as many examples as you need. These pages are to illustrate method.

Spend at least five to ten minutes twice daily, once in the morning and once before bed. This can be done on the way to the supermarket, or out in the park, it does not have to be formalised. It can be done pointing at trees or parking meters, or counting packets on a supermarket shelf.

The time taken to learn a skill will vary from child to child according to a variety of factors, the main ones of which will probably be intelligence, concentration, obedience, sufficient sleep and food, calmness in the surrounding atmosphere, and the rationality of the person supposedly teaching the child.

Bear in mind that the child will have ‘good’ days and ‘bad’ days in learning. One day, numbers, counting or addition skills thought to be committed to memory the previous day seem to have been forgotten, and so forth. Be patient - this seems to happen with many children and is probably a mechanism of learning that we do not yet fully understand. Do not lose your temper or become irrational. However, a little pushing may trigger the memory or make the child put more effort into its work.

Help on writing down addition sums.

Teaching rationally

You can check the child’s progress by maintaining records. Records should be kept accurately and should not be distorted by irrational emotional involvement. For example, you may find yourself distorting your records because you have convinced yourself - from some wish that the child achieves quicker than it does, or simply by chopping corners - that the child really does know something which it does not. Such behaviour will not help the child. It may make you feel a little better temporarily, but will certainly be bad for the child. Adopting such an approach will inhibit their ability to learn and in other ways disturb the child. If you can not control yourself and learn yourself, you are better leaving the child to the fate of the state teachers, even though they are, in our experience, almost invariably sub-competent.

Above all, be calm and quiet and patient, but do not allow the child to misbehave, to take advantage of you, or to be a nuisance. The child is getting something from you, not vice versa. Neither over-push nor under-push, find the balance for each individual child.

end notes

1. To be useful, a set of Cuisinaire rods including at least 100 white (one-unit) rods is needed.
   
   Cuisinaire rods are available in the USA from ETA/Cusinaire in both plastic and in wood.
   The “small group” moulded plastic tray of 155 rods (with about 60 white rods) costs $19.95 for plastic rods and $23.95 for wooden ones.
   Six plastic trays of 74 rods each (22 white rods per tray) costs $49.95 for plastic rods and $65.95 for wooden ones.
   
   In the United Kingdom, German look-a-like wooden rod sets are available from Wooden T.O.T.S. A set of 300 pieces in a wooden box costs £15.00. The company will send sets abroad. This set includes about 175 white blocks.
   
   This is an ‘original’ box of Cuisinaire rods:

email email_abelard [at] abelard.org

© abelard, 2009, 02 may

all rights reserved

the web address for this page is https://www.abelard.org/sums/teaching_number_arithmetic_mathematics_counting_addition.php

1515 words
prints as 6 A4 pages (on my printer and set-up)