Gödel’s confusions— METALOGIC A

A1—Gödel and sound sets

A2—Gödel and sound numbers

A3—Gödel and the ‘paradoxes’
A4—The Return of the Gödel

Box: Two great errors of human reasoning

Generalisation
Projection

Numbers as labels
So what has Gödel done?
Recap.
Levels of relaxed rigour
Endnotes
Bibiliography
C O L O U R K E 'Y'

Rigour
Consistency

‘Absolute’ consistency
Relative consistency
Just how many numbers are there?
Just what is the biggest number?

Countability and numbers
Chopability, green and proveability
Just what is a number anyway?

Rigour

98. To proceed any further with analysis of the confusions of Gödel it is necessary to begin to relax rigour.
99. By relaxation of rigour, I mean a degree of distancing from empiric evidence. For example, to start discussing the attributes of ‘unicorns’, I would be in some manner constrained to act as if unicorns existed in the real world.
100. A peculiarity of the religion widely called mathematics is to call it ‘rigorous’ if one follows the rules decided by ‘mathematicians’! In other words, should a ’theory’ start from an assumption, such as ‘there are unicorns’, and then at some point a statement occurred which did not ‘fully’ agree with the original assumption (that unicorns exist), the statement would be regarded as an inconsistency (with the original assumptions) and the line of discussion would be claimed to be not rigorous!
101. Thus does mathematics far more resemble a codified superstition than it resembles ‘science’. Science tends to appeal to evidence, while mathematicians, like priests, tend to appeal to ‘authority’: theirs! Note how mathematics thus mirrors an approach to ‘knowledge’ similar to that of the ontological argument rather than to the investigation of gravity or the conditions for heavier than air flight.
102. To follow through the game of Gödel, and all those who imagine that they understand or agree with Gödel,
     the first level of rigour reduction that I will indulge (accept) is the assumption that it is possible to separate objects ‘completely’.
     That is, I will pretend that the ’law’ of the excluded middle has real meaning. It has not, but I will pretend that it has, just as I could pretend unicorns were real creatures. Many mathematicians unconsciously indulge this sort of let’s pretend every day at the office. For further background, read the error called‘equality’, the error called‘zero’or‘not’or‘negative’ and the error called‘infinity’ in Why Aristotelian logic does not work.
103. The second level of rigour reduction that I must indulge is the assumption that any ’two’ of these ‘objects’may be ‘equated’.
     This includes the notion that ‘objects’ may be matched or ‘mapped’ ‘one’ to ‘one’. This means that, given a group of turkeys and another group such as a group of pencils or formulae or, for all I can gather, a group of unicorns, one may line up the turkeys and place one pencil in front of each turkey until you run out of turkeys. If you happen to run out of pencils, or even unicorns, at the ‘same’ time, you can be sure that you have the ‘same’ number of turkeys aspencils.
     Advice: if carrying out this experiment, it is helpful if you can persuade the turkeys to keep still.

Consistency

104. Ideas of ‘consistency’ are built upon two non-empiric axioms:
     the ‘idea’ of ‘separation’ and the ‘idea’ of ‘equality’.
105. These ideas are then applied to what are supposed to be two versions of consistency: ‘absolute’ consistency and relative consistency. I shall soon show that ‘both’ forms are, in real terms, relative ‘concepts’.

     ‘ABSOLUTE’ CONSISTENCY

106. Absolute consistency is supposed to exist if two ‘structures’ can be mapped one to one in ‘all’ details. But, of course, the details mapped are chosen by the individual ‘mathematician’ and the precedence given to any details is selected: the details do not come from the stars with labels saying, “I am a relevant detail”.
107. For example, ‘triangles’ are addressed by ‘their’ vertices and sides; little attention is paid to the ink out of which they are drawn, or the words used to refer to the vertices or the sides. We are calmly assured by ‘mathematicians’ that these issues are ‘not relevant’, or that the triangles are somehow ‘abstract’.
108. There is no such thing as an ‘abstract’ triangle any more than there is a ‘perfect’ circle, the idea of the triangle, at the very least, resides in the real brain of the mathematician, there encoded in real molecules and activated by real electrical activity within the brain.
109. If the mathematician can list every combination of sides and vertices and map each and every ‘one’ them to a bunch of words called ‘axioms’, then the mathematician will pronounce the system ‘absolutely’ consistent.[1] Remember, the mathematician chose the words, and chose to what they should refer, and decided all this assembly would sit still while this process was carried out. (See also numbers or objects.)
110. Note that this process is, in fact, relative; it relativises the description to the triangles.
111. A triangle may be described in Mandarin Chinese and in English, and the two descriptions mapped. The triangle is a way of describing a ‘flat’ surface of a table or a country or a map. All are descriptions of reality. None of them ‘are’ the reality they are designed to describe. None of the descriptions are the ‘same’. As ever, if the term ‘same’ is used, it means, “ Right now, I don’t care about the differences”, and that is all that it means or can mean. (See also the error called ‘equality’.)
112. The way in which counting is applied is arbitrary choice. Mapping is therefore also arbitrary.

RELATIVE CONSISTENCY

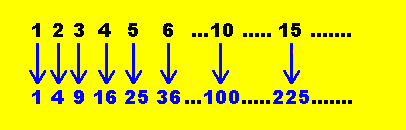
113. Cantor based his work on a way of ‘counting’ called one to one mapping. With a little finagling, he ‘proved’ that there were just as many square numbers as ordinary counting numbers. That is, there are as many ‘square’ numbers like 1,4,9,16,25 etc as there are numbers like 1,2,3,4,5 etc; [2] his reasoning being that for each number such as 10 or 15, you can form a number such as 100 or 225! [diagram below.] Attend carefully to the dot-dot-dot at the end of each row, which is designed to suggest that this process just goes ‘on and on’. This is non-sense, but it is rather subtle nonsense and it has oft been repeated since. Hilbert, another of the modern high priests of maths, referring to this wondrous achievement and seeing the opposition of more down-to-earth workers said, “No one shall drive us from this paradise which Cantor has created for us”. [3] I intend to do just that.

JUST HOW MANY NUMBERS ARE THERE?

114. Consider ‘a’ plant for manufacturing cars. There are plans, which are followed in the production process, and there is the factory system that acts upon matter, such as steel and plastic, to form and assemble the cars.
115. With numbers, there also exist a series of rules to be followed, often termed an algorithm, (see also lists of instructions) and there is a human who carries out the process and writes down or ‘thinks’ of the various real numbers.
116. Consider some super mathematician who sets about writing numbers down, starting at the number one and continuing until they ran out of chalk or ink. So they go down to the shops for more ink, and then they run out again. In due course, every factory in the world is devoted to producing more ink, and ever more writers of numbers are drafted. ‘Ink’ is manufactured from iron filings and cow dung, but still more numbers can be produced. Space ships are sent out for more matter.
117. Problem: eventually, whether assuming a room or a planet or a finite universe of resources, you will run out of matter with which to write numbers. Whatever else, you will get rather tired, or die, or consider, “Damn this for a game of soldiers, I’d rather have a meal, or even watch football, than this”. And this is assuming that you hadn’t already used up the football and the meal for writing numbers. Thus, the idea of counting ‘for ever’ is not viable in the real world. The common concept of a ‘completed’ ‘infinity’ is not empirically viable. (For more detail, see the error called ‘infinity’, and also the Logic of ethics, end-note 6).
118. We have the nice rules for constructing numbers but, just like the car manufacture, any particular number still has to be manufactured out of real matter, taking real effort and real time (see also box II - relativity)

JUST WHAT IS THE BIGGEST NUMBER?

119. Strangely, we may, with our algorithms, manufacture numbers beyond all useful meaning. We may produce a number greater than the number of ‘grains’ of sand on all the shores of this planet, or even a number that is greater than the number of ‘atoms’ in the known universe. Such an example has been suggested by a mathematician and named a ‘googol’.[4] It is defined as 10 raised to the power of 100, that is 10¹⁰⁰. This is therefore a number rather like the word ‘unicorn’ and like some uses of zero, in that it does not point at anything in the real world (further discussion to be found in the error called ‘zero’...).
120. Be clear that we can manufacture arbitrary numbers, ‘way out there’, far beyond any number we could ever construct if we start from the number one and continue to count until we run out of matter.
121. Further, because we can produce such a number does not mean that the number indicates anything real beyond ‘the’ number recorded upon the paper or an electronic billboard. The number can easily have a similar status to the word ‘unicorn’.

Countability and mapping

122. To recap: Cantor has defined number in terms of what may be mapped to what else. (See also paragraphs 106 and 113).
123. A typical example is the one referred to above, where Cantor maps the integers to the square numbers. Cantor appears to misunderstand that, because he has rules for producing any particular number or ‘square’, just as the car manufacturer has plans for producing various particular types of car, it does not follow that there are somehow ‘out there’ the ‘same’ number of square numbers as there are integers. Every square number, and every integer, must first be constructed in some real manner out of matter.
124. Just which numbers humans choose to construct at any particular time is a matter of current decision. The numbers are not somehow ‘out there’ waiting to be picked up like so many stones upon a beach.
125. The matter of mapping one number to another is little different to mapping turkeys to pencils or cars to gloves; but first you must always catch your turkeys or manufacture your cars.
126. Cantor’s mapping thus becomes a mere tautology [5] which amounts to:
     If I decide to manufacture the number 2, I can also then manufacture a number 4 (which I will call the square of 2) by applying a particular set of instructions. This is a piece of information we already had, once ‘square’ had been defined to mean, “Multiplying a number by ‘itself ’” (see also the error called ‘equality’). It does not follow meaningfully that “there are the ‘same’ number of square numbers as there are integers” at this particular moment of time. Without care, it is rather easy to come to foolish conclusions if you do not map words very carefully to real matter.
127. The existential [6] statement that there are the ‘same’ number of squares as there are integers is an empiric claim that has the potential to be tested by going out and counting the damn things. If anyone is inclined to carry out this investigation, I am very willing to bet good money that they will not find the same number of each type of object. I would make a fair guess that they will find rather more integers lying around than square numbers. Those who claim that the numbers are ‘the same’ when used for manufacturing both integers and squares have clearly confused potential with fact: A parallel, or should I say a mapping, with the ontological argument.

advertising disclaimer

Chopability, green and proveability

128. Remember, ‘chopability’ relies upon a tree and a human to chop the tree . I am asserting that any word, in order to have meaning, must clearly refer to delineated ‘objects’ or ‘parts’ of real matter. The word ‘chopability’ refers to the assemblage, not to the tree alone. Further, the term is asserted of the future, the tree ‘is’ not chopable, instead, it is possible for the human to chop the tree. Only when the tree is actually being chopped do we have a real world ‘happening’ or ‘object’, i.e. the assembly comprising the human, the axe and the tree in process of movement and change over a period of time. The act is the object; the object is the act (see also universals and individuals).
129. Green does not require a human participant. As a child in the playground, one hears the triviality, “Does a tree falling in the forest make any sound?” Clearly sound waves are generated by the crashing of the tree, the fact that there is no human to hear the sounds and call the sound by the word ‘sound’ has no bearing upon the physical realities. The question itself is an interesting example of anthropomorphic (human centred) ‘thinking’; to imagine that somehow the world requires human validation in order to exist is hubris indeed.
130. Likewise ‘green’ light exists quite independently of any human participant. The leaves of the tree reflected light in the wavelength we now call green long before humans were available to name ‘green’ as a somehow ’separate’ ‘part’ of ‘the’ spectrum. Green is the leaf object reflecting the light, In terms of what we habitually refer to as green, an object is ever required to reflect or transmit the green to our eye and brain.
131. Rather ‘differently’, before ‘proveability’ can occur, we must have formulae written upon paper by humans, we must have rules to manipulate those formulae, and we must have individual humans to define, as carefully as they may, (see also box I – iteration) what they each mean when they use the term ‘provable’(see also numbers or objects).
132. Usually, with the tree and with chopable and with green, we may not have to be quite so cautious as we need to be with ‘proveability’. For, in those cases we are not normally discussing the ‘precision’ (see also the error called ‘complete’) of communication, whereas with ‘proveability’ the very issue of such imagined clarity is being ‘analysed’. Thus we must be particularly careful to indicate what we mean when we use the term ‘provable’, to be clear just what real object it is to which we are attempting to refer and at just which point in time.
133. Remember that when I ‘spoke’ of ‘chopability’, I was careful to note that the present object was the tree in process of being chopped, not the mental images that may have occurred before (or even after) the act of chopping.For clarity, it is essential that time frames be kept constantly in awareness (see also ways of viewing the world).

Just what ‘is’ a number anyway?

134. This is a rather more trying question than might at first appear! Gödel and others have attempted to separate (form ‘two’ categories):
     1) an idea of number as “the number ‘itself ’”! and
     2) ‘talking about the number’.
     This just will not do! This ‘separation’ is not ‘sufficiently’ clearly established or defined. To confuse things a little further, though I am betting that was not their intention, they refer to the ‘talking about a number’ category as the numeral and the number ‘itself ’ as the number.[7] The ‘numeral’ is also often called ‘the label for the number’.
135. While discussing chopability, green and even some aspects of numbers above, I have often used the word ‘is’. In fact, this is rather sloppy language and now I am going to have to be rather more careful with my examination of ‘just what is a number’. The word is, is now appearing in red as a traffic warning sign for ‘danger’, in this case dangerously sloppy language (if this is assuming too much for you, see also the error of the verb ‘to be’ and make sure that you are reasonably clear about the difficulty).
136. ‘A number’ is a very broad ‘generalisation’ or ‘universal’(for more, see universals and individuals).

Two great errors of human reason

1. Generalisation

To generalise is to believe that what is true of one object or group of objects is true of another, without careful examination of the objects in question.

It is to believe that any two objects are ‘the same’ in any real sense.

Treating objects ‘as if ’ they are ‘the same’ may well work in some sense for you when the factual real differences are of little concern to you at that ‘moment’. But every action you take in the real world with ‘those’objects is a ‘new’act.

Remember, your life is a continuum, and ‘the’ objects also are continuous ‘in’ reality. Separations are, at least in part, ‘illusion’, as Manjushri and Heraclitus understand.

‘Generalisations’ may be very useful and save you time and thought, but they are a trap waiting to happen. Remain aware that your generalisations are not ‘ever’ secure.

See also universals and individuals.

The problems with generalisation grow with the complexity of the ‘objects’ being examined or discussed. The most complex object yet on this planet is another human. Every person is different; forgetting that is not a good idea.

2. Projection

‘Projection’ is to assume that another person thinks the ‘same’ way you do. It is assuming that they have the ‘same’ objectives. It is assuming that when another uses a word, it means the ‘same’ to you as it does to them. It is to assume that when you use a word, it means the ‘same’ to them as it does to you.

Projection is to assume that when another person does what you imagine that you would have done in ‘a’ situation, that they are doing it for the ‘same’ reason/s that you would have done it.

It is to assume that you ‘agree’ or ‘disagree’ because you think the words are the ‘same’ (see also excluded middle).

The idea of ‘same’ is false to reality; it is just a term meaning, “I don’t care about the differences right now”.

See also the error called ‘equality’’.

137. To repeat, a ‘number’ is a very broad generalisation; as such, it does not ‘exist’ in the world outside of your head. There is no such thing as ‘trees’ outside your head. Look, there is a tree and another tree and yet another tree over there; each tree is different. The trees are ‘part’ of the world. There is but ‘one’ world. Each ‘is’ is a choice by an individual, in this case, ‘me’. See also counting is not simple and numbers or objects, you may need to check these sections before proceeding.
138. Assertion: when you count, you run a small program, or series of instructions, in your head that you learned how to do when you were rather young. You decide which ‘bits’ of reality you are going to regard as ‘objects’, and then run through the magic ordered grunts (called numbers) that you learnt in the nursery.
139. This grunting pattern is[8] widely taught in western and other cultures. It is a very useful way of communicating our approximate needs and ‘ideas’ to others. But the numbers are grunted on each separate occasion. There is no great number in the sky. Kronecker, another great mathematician said of mathematics, “god made the integers, all else was made by man”.[9] I assert that Kronecker under-estimated humankind and over estimated numbers.
     
     
140. Remembering that any word, in order to have meaning, must point at real matter and also remembering numbers are also words:
     
     A ‘number’ can be:
     
     
     1. that which is written or said, such as the number 5 now on your screen.
     Else ‘number’ must refer to:
     
     2. the program in your head or the process of running that program when you are counting, perhaps for the moment I will think of the latter as a number generating machine or program.
     What ‘the number’ is not[10], is
     
     3. some vague ‘something’ ‘out there’.
        
        
     We now have at least three potential meanings for the word ‘number’, the last one of which is clearly unsound.
     
     
141. The program in my head is encoded on different matter from the encoding in your head, even though we may both write down numbers on paper with rather similar shapes, (see also in the world of thought as ‘immaterial’) after each separately ‘counting 5 trees’. We may ‘agree’ not to concern ourselves with these various differences, but the differences are very real.
142. So, which ‘thing’ is the ‘numeral’ and which ‘meaning’ or ‘object’ is to be called the ‘number’? Here abouts, things get a little problematical, for mathematicians appear too confused upon this issue to offer some widely accepted ‘definition’. We may guess at just what Gödel or other mathematicians might have had in their own minds when referring to number or numeral, but, because of their own apparent confusions, this seems to me a not necessarily profitable project.
143. I am asserting that there is no number out there on a sky hook, but only some often rather vague idea of what numbers are in the minds of the likes of Kronecker and Gödel, Nagel and Newman and others. Thus, I am led to the conclusion that the attempt to separate ‘numbers’ from ‘numerals’ is ill-defined.The ‘proofs’ of Gödel, however, ride upon such an imagined ‘separation’.

Numbers as labels

144. There is a constant assumption that ‘mathematics’ is somehow ‘different’ from the rest of language: that is a false and often damaging perception. The false split is reflected in the education system, where even separate classes are held for the ‘two’ ‘subjects’.
145. When we label a price in a shop or count to 8 trees, we put a label upon those ‘objects’. When we then refer to the label which we placed upon the ‘objects’, we may also term that label as an object with the number written upon it. The number written in ink upon the label seems to be what mathematicians are attempting to indicate when they use the word ‘numeral’ (see above).
146. The actual process of counting, prior to deciding upon which label to affix to the ‘object/s’ (whether on a label or in the counting person’s head), seems not to be examined with much focus by Gödel. Instead, Gödel seems to be confused into thinking that there is, somewhere ‘out there’, some object in the mind of god for each and every number, rather like the standard kilogram kept in Paris. These unicorns he seems to be calling ‘numbers’. No, I don’t think so!
147. To investigate just what is going down in the Gödel ‘theorems’, we must make a very careful study of the terminology, ensuring at each point just what real object we are indicating. Even if we are to discuss Gödel’s unicorns, it would be wise to decide which set of numbers were in the possession of god and which were mere human copies.
148. If god has gotten itself a standard set, I intend to stop at assuming that he has only one such set, rather than assuming that we go to the god shop for each new copy. We can as well make our own, perhaps inferior copies, with our own pencils or chalk, but in each such case we must decide which is the original and which are the copies, and just how many copies we have to hand, in any particular discussion.[11]
149. Russell and Whitehead set up a particular notation, based upon the notation of Peano for doing sums or, if you prefer it, ‘mathematics’, in Principia Mathematica (1910-13). Gödel invented a system of changing the symbols of the notation back into ‘numbers’! This system is often called “Gödel numbering”; it would be better called “Gödel labelling”. The ‘two’ notations are mapped onto one another, in such a manner that you may write down a formula in one notation and reliably translate it into the other notation. One system looks like numbers, the other a few rather different squiggles including some ordinary letters.[12]
150. Now, remembering the section on Cantor’s mapping up above, (see paragraphs 113, 122 and 126 above), it is relevant to note that these labels that Gödel developed were manufactured to look like the numbers held by god, and even to bear some relationship to some of the numbers in god’s original set. Gödel, in fact, only bothered with god’s ‘prime numbers’, so leaving considerable quantities of god’s originals unused and unattended. Thus, the situation was very similar to Cantor’s game of attempting to make one group of numbers somehow ‘equate’ with another set by, for example, actually calling them ‘numbers’ instead of ‘just’ labels.
151. It is useful to point out that humans have often been rather fascinated by ‘prime numbers’, in rather the manner that children are fascinated by ‘collecting’ car or train numbers or bus tickets with serial numbers that add up to 7 or some such.
     In Gödel’s case, the primes turned out to be rather useful for avoiding confusion with his labelling system. He was also able to do some ‘factorisation’ within his strange set of number-labels, making his factoring look somewhat like the factoring that can be done if you play with a more extended set of numbers, rather than just with a few specially selected ones.[13]
152. So now we have a labelling system, which I intend to call “Gödel labelling”; and our more usual, grunt grunt grunt, one two three, sort of labels we use for shop prices, counting ‘trees’, counting ‘votes’ and even electrons, according to our needs and moods. Yes folks, however we get there, words—whether wecall them numbers or Gödel-numbers or even timbuctoos—when used sanely, are primarily used as labels.

So, what has Gödel done?

153. In a series of  formulae comprising a proof: that is a list of  formula terminating in a formula said to be a proved formula, Gödel has mapped his Gödel-‘number’-labels to formula and groups of  formulae; and then treated the labels as if they were numbers.
154. He has then claimed that the prime-number-labels he has used are deconstructible (factorisable) in the positive integer number system,[14] in such a manner that the prime-number-label that he associates (maps) with a proved formula is a definable fraction of the prime-number-label that can be associated with a ‘proof ’.
155. That is, a group of related formulae, of which a particular formula is said to be the proved formula, is assumed to have an arithmetic relationship one to the other. In short, Gödel claims that the meta-mathematical statements about arithmetic can thereby be mapped or ‘reflected’ within the integer arithmetical system.
     As an example, in a typical factorisation deconstruction in the integer system, the number 2 x 3 x 5 x 7 x 11 x 13 x 17 has factors such as the numbers 2 x 3 or 13 x 17 or 5 x 13. In arithmetic according to the rules, 2 x 3 is a number; that is 2 x 3 may also be called the number 6.
156. Gödel claims that he can (therefore!) reproduce the metamathematical statements about integer arithmetic within the expressive symbols of the integer arithmetic.
157. Let us look a little further:
     The prime numbers form only a part of the integer system.
     If you count in integers, the counting goes thus: 1,2,3,4,5,6,7,8, etc.
     If you count in primes, it goes thus: 2,3,5,7,11,13,17, 19, etc.
     In other terms, when mapping the two labelling systems, the integers and the primes to one another, 1 maps to 2, 2 maps to 3, 3 maps to 5, 4 maps to 7 and 5 maps to 11, etc. This mapping also contains a hidden assumption that we may ‘count for ever’. I return to this in Metalogic-A3: Gödel and the ‘paradoxes’.

158. In the new system of supposed primes, therefore, the apparent number ‘7’ (the fourth number in this counting system using primes) is no longer a prime in the normal sense. For as you will see from the diagram, 7 is now the fourth number and as such, it is now the square of ‘3’! Or, if you prefer, 7 is the number after (the successor of) 5, and 7 is the successor of the successor of 3. This continues onward with the two series ever parting company.
     Assuming the original meaning of the term ‘prime-number’ is maintained and that we are not going to change the meaning of ‘prime number’, as we move from the meaning of prime number as the Gödel-‘number’-label in the metamathematics to its supposed meaning in the integer arithmetic, the ‘meanings’ of the different labelling systems alter. The number labels just look similar when written on paper.
159. I am unsure that this magician’s slight of hand is entirely within the ‘rules’ of the game called ‘arithmetic’. Even should you decide that you are happy with the trick, remember that I am still going to keep a very close eye on each of your copies of each ‘number’.

Recap.

160. You will note that, in order to agree on just which numbers or labels are being used, first you and me gotta have a parley. It is not enough to say that Gödel says or means this or that. Gödel ain’t here to ask ‘exactly’ what he did mean or exactly what he does think; as like as not, he is up there above the clouds playing with god’s original set. For us ‘two’ to agree to proceed, we must first be as clear as maybe on just what each of us means by each term. Note well that this is an iterative process, not a blind acceptance of absolutes or even the authority of Kurt Gödel.
161. The term ‘equals’ is often meant and received as assertive: that is, it can be used as ‘authority’ ploy rather than in a communicative mode. I am not prepared to accept such terms without close attention and examination. Whether you accept them uncritically is of course your choice. When Kurt claims that two number labels are ‘equal’, my mark-5 crap-detector gives a little bleep. He may not care about the real differences but I may, therefore first I will take a careful look before moving onward down the slippery slope.
162. I confess that, at this point, I cannot claim to feel the footing is entirely secure. I have reduced rigour in order to proceed on several occasions, and now I have what looks to me like a yawning hole in the mapping system. Remember that mapping is a form of labelling; we put a label on that (approximate) thing over there, a label like ‘tree’ or ‘one’. It is very necessary that we do not confuse the real label with that real thing (refer also to numbers or objects) ‘out there’ upon which we stuck the label.
163. Your finger cannot point at itself.
164. I am very unconvinced that Gödel has sufficiently distinguished, or even clearly categorised, his labels. But I shall still continue to observe just what he then does with the mess of pottage that by now he is stirring.
165. Perhaps the inconsistencies generated by Gödel are mere tautology? Gödel is said to have been worried that he had merely unearthed a paradox.[15] Methinks you may have had a point Kurt, but what a ‘paradox’!(Read more on this in Metalogic A4—The Return of the Gödel).
166. Gödel’s ‘proofs’ well and truly cut the support from under the confidence of many of his contemporaries and a host of others since, and that can be no bad thing. I have even ‘seen’ it said that Gödel showed that mathematics was the only religion that could prove that it was in error (see introduction to Gödel and sound sets).

Levels of relaxed rigour

167. We now have accumulated several levels of relaxed rigour:
168. we have allowed the notion of  ‘the excluded middle’;
169. we pretend the ‘equality’of separate ‘objects’;
170. we must also now imagine we can count ‘for ever’;
171. we must believe that the mappings necessarily make sense, where in fact they may well not (see paragraph 158 with comment at paragraph 159);
172. all the while, keeping in mind that the sentence upon which the Gödel statements are based contains structural problems (see paragraphs 50 and 51 of Gödel and sound sets).

1. problems with the verb ‘to be’ (for a more full discussion, see the error of the verb ‘to be’), and
2. clarity of definition of the term ‘provable’ (in note to paragraph 83 in Gödel and sound sets), I return to this with more detail in Metalogic A4—The Return of the Gödel.

Continue Gödel’s confusions with
A3—Gödel and the ‘paradoxes’
A4—The Return of the Gödel

Endnotes

1. For instance, see p. 16, Nagel and Newman.
2. This process was noted by Galileo in 1638. It is also referred to as Galileo’s ‘paradox’. This method was also used by Dedekind in 1888 as a property to distinguish ‘infinite’ sets from finite sets. Cantor’s work dates from 1874. He was the first to apply this idea systematically to ‘infinite’ collections.
3. Barrow, p.213
4. Kasner. He also defined (1940) a googolplex as 10 raised to the power of a googol. For the word ‘googol’, Kasner got his 9 year old to think of a name for a very big number. Incidently, we also now have a very good search-engine on the Web called Google. Note the difference in spelling.
5. Tautology means saying the same thing twice in different ways.
6. Assertion of existence, statement that the supposed object exists.
7. For instance, see p. 83, Nagel and Newman.
8. In this case ‘is’ is being used to state an empiric (observable) fact or datum.
9. Barrow, p.188.
10. See also section 8 of Why Aristotelian logic does not work.
11. For those who wish to worry this a little further see comment re Abelard in section 2 of Why Aristotelian logic does not work.
12. For instance, see p. 70-1, Nagel and Newman.
13. It is interesting that very big prime factors are now used in encrypting messages. Amazing the uses humans can find for all sorts of strange things they find lying around. They even make necklaces of seashells after the original owners have moved on, while others have used sea-shells for money..
14. The numbers 1,2,3,4 etc; the whole numbers, sometimes called the natural numbers. By definition, the natural numbers are the positive integers and the ‘number’ zero (0). The integers are the natural numbers plus the negative integers -1,-2,-3 etc. In both cases, zero is taken as a ‘number’, this inclusion of zero as a ‘number’ undifferentiated from other integers, I regard as dubious (see the error of ‘zero’, ... and sections 3 & 4 of Comparing predicates, relational strengths).
15. A quote from Stanislaw Ulam, cited in Regis, p.66 states:
    Gödel suffered from “a gnawing uncertainty that maybe all he had discovered was another paradox à la Burali forte or Russell”.

Bibliography

COLOUR KE'Y'

Generally,
Blue links to parts of this document
Orange links to Bibliography and to other bibliographic information
Green gives links to sites external to  www.abelard.org
Yellow gives links to other documents within  the  abelard site. Document titles are in italics, whilst section titles are normal/in roman type.

Magenta highlights points of special note
Red attracts attention to important points
[Light green indicates the capitula under which Abelard was tried - not used in this document]

All links are underlined
Words in single quotes emphasise less than close, meaning for those words, or a dubious usage.
Words in italics are words being used as label for other words, for instance the word word.

email email_abelard [at] abelard.org

© abelard, 2001, 28 January

all rights reserved

the address for this document is https://www.abelard.org/metalogic/metalogicA2.php

6010 words
prints as 11 A4 pages (on my printer and set-up)